NumPy库入门

掌握表示、清洗、统计和展示数据的能力

简介

NumPy是一个开源的Python科学计算基础库，底层实现是用C语言实现，实现数组时底层提供高效运算性能。

  • 一个强大的N维数组对象ndarray
  • 广播功能函数
  • 整合C/C++/Fortran代码的工具
  • 线性代数、傅里叶变换、随机数生成等功能

Numpy是SciPy、Pandas等数据处理或科学计算库的基础。

1
2
#引用
import numpy as np

数据表示

数据的维度

从一个数据到一组数据，一个数据表达一个含义，一组数据表达一个或多个含义。维度是一组数据的组织形式。数据之间的关系。

一维数据

由对等关系的有序或无序数据构成，采用线性方式组织。（对应列表、数组和集合等概念）

列表和数组

一组数据的有序结构，区别：

列表：数据类型可以不同。

1
3.14,'pi',3.1404,[3.1401,3.1349],'3.1376'

数组：数据型相同

1
3.1413，3.1313，3.1234，3.1451，3.5161

二维数据

二维数据由多个一维数据构成,是一维数据的组合形式。

排名 学校 总分
1 清华 100.0
2 北大 99.8
3 浙大 98.8

多维数据

多维数据由一维或二维数据在新维度扩展形成。2023->2024，时间维度。

排名 学校 总分
1 清华 100.0
2 北大 99.8
3 浙大 98.8
排名 学校 总分
1 清华 100.0
2 北大 99.6
3 浙大 98.7

高维数据

高维数据仅仅利用最基本的二元关系展示数据间的复杂结构。

1
2
3
4
5
6
7
8
9
10
11
12
{
	"firstName":"Tian",
	"lastName":"Song",
	"address":{
		"streetAddr":"中关村南大街5号",
		"city":"北京市",
		"zipcode":"1000081"
	},
	"prof":["Computer System","Security"]
}
#键值对组织
#没有数据规整的组织方式，却有数据间的包含关系、数据间的并列关系以及数据间的属性关系等，形成了数据的组织方式

如何表示

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#一维数据
[3.1413，3.1313，3.1234，3.1451，3.5161]有序、列表
{3.1413，3.1313，3.1234，3.1451，3.5161}无序、集合

#二维数据
[[3.1413，3.1313，3.1234],
 [3.1234，3.1451，3.5161]]列表

#多维数据
列表

#高维数据
字典类型或数据表示格式(JSON、XML和YAML格式)
dict = {
    "firstName":"Tian",
    "lastName":"Song",
}

数组对象:ndarray

  • 数组对象可以去掉元素间运算间运算所需的循环，使一维向量更像单个数据。

  • 设置专门的数组对象，经过优化，可以提升这类应用的运算速度。

  • 观察：科学计算中，一个维度所有数据的类型往往相同。

  • 数组对象采用相同的数据类型，有助于节省运算和存储空间。

  • ndarray是一个多维数组对象，由两部分构成：

    • 实际的数据
    • 描述这些数据的元素据（数据维度、数据类型等）

    ndarray数组一般要求所有元素类型相同（同质），数组下标从0开始。

例：计算$A^2+B^3$，其中，A和B是一维数组

1
2
3
4
5
6
7
8
9
10
11
def pySum():
	a = [0,1,2,3,4]
	b = [9,8,7,6,5]
	c = []
    
	for i in range(len(a)):
		c.append(a[i]**2 + b[i]**3)	
		
	return c

print(pySum())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np

def npSum():
	a = np.array([0,1,2,3,4])
	b = np.array([9,8,7,6,5])
	
	c = a**2 + b**3
	
	return c
	
print(npSum())

#np.array()生成一个ndarray数组
#ndarray在程序中的别名是：array
#np.array()输出成[]形式，元素由空格分割
#轴(axis):保存数据的维度	秩(rank):轴的数量

ndarray对象的属性

属性 说明
.ndim 秩，即轴数量或维度的数量
.shape ndarray对象的尺度，对于矩阵，n行m列
.size ndarray对象元素的个数，相当于.shape中n*m的值
.dtype ndarray对象的元素类型
.itemsize ndarray对象中每个元素的大小，以字节为单位 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
In [22]: a = np.array([[0,1,2,3,4]
					[9,8,7,6,5]])
    
In [23]: a.ndim
Out[23]: 2
    
In [24]: a.shape
Out[24]: (2,5)
    
In [25]: a.size
Out[25]: 10
    
In [26]: a.dtype
Out[26]: dtype('int32')
    
In [27]: a.itemsize
Out[27]: 4
数据类型 说明
intc 与C语言中的int类型一直，一般是int32或int64
intp 用于索引的整数，与C语言中ssize_t一致，int32或int64
int8 字节长度整数，取值：[-128,127]
int16 16位长度整数，取值：[-32768,32767]
int32 32位长度整数，取值：[$-2^31,2^31-1$]
int64 64位长度整数，取值：[-2^63,2^63-1]
uint64 64位无符号整数，取值：[0,2^64-1]
float64 64位半精度浮点数：1位符号位，11位指数，52位尾数
complex64 复数类型，实部和虚部都是32位浮点数，实部(.real)+j虚部(.imag)
… …

对比：Python语法仅支持整数、浮点数和复数3种类型，且其中整数类型是没有取值范围划分的，浮点数和复数仅有一种。

支持那么多种数据类型？

  1. 科学计算涉及数据较多，对存储和性能都有比较高要求。
  2. 对元素类型精细定义，有助于NumPy合理使用存储空间并进行优化性能。
  3. 对元素类型精细定义，有助于程序员对程序规模有合理的评估。

可由非同质对象构成

非同质ndarray对象无法发挥NumPy优势，尽量避免使用。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
In [61]: x = np.array([[0,1,2,3,4],
					 [9,8,7,6]])

In [62]: x.shape
Out[63]: (2,)

In [63]: x.dtype
Out[63]: dtype('O')  #非同质ndarray元素为对象类型。

In [64]: x
Out[64]: array([[0,1,2,3,4],[9,8,7,6]],dtype=object)

In [65]: x.itemsize
Out[65]: 4

In [66]: x.size
Out[66]: 2

ndarray数组的创建和变换

ndarray数组的创建方法

  1. 从Python中的列表，元组等类型创建ndarray数组。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    x = np.array(list/tuple)
    x = np.array(list/tuple,dtype=np.float32)
    # 当np.array()不指定dtype时，NumPy将根据数据情况关联一个dtype类型

    In [32]: x = np.array([0,1,2,3])	#从列表类型创建

    In [33]: print(x)
    [0 1 2 3]

    In [34]: x = np.array((4,5,6,7)		#从元组类型创建

    In [35]: print(x)
    [4 5 6 7]

    In [36]: x = np.array([[1,2],[9,8],(0.1,0.2)])		#从列表和元组混合类型创建

    In [37]: print(x)
    [[ 1. 2.]
     [ 9. 8.]
     [0.1 0.2]]

  2. 使用NumPy中函数创建ndarray数组，如：arange,ones,zeros等。

    | 函数 | 说明 |
    | ————————— | ——————————————————————— |
    | np.arange(n) | 类似range()函数，返回ndarray类型，元素从0到n-1 |
    | np.ones(shape) | 根据shape生成一个全1数组，shape是元组类型 |
    | np.zeros(shape) | 根据shape生成一个全0数组，shape是元组类型 |
    | np.full(shape.val) | 根据shape生成一个数组，每个元素值都是val |
    | np.eye(n) | 创建一个正方的n*n得矩阵，对角线为1，其余为0 |

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    In [73]: np.arange(10)
    Out[73]: array([0,1,2,3,4,5,6,7,8,9])

    In [74]: np.ones((3,6))
    Out[74]: array([[1.,1.,1.,1.,1.,1.]
    			   [1.,1.,1.,1.,1.,1.],
    			   [1.,1.,1.,1.,1.,1.]])

    In [75]: np.zeros((3,6),dtype=np.int32)
    Out[75]: array([[0,0,0,0,0,0],
    			   [0,0,0,0,0,0],
    			   [0,0,0,0,0,0]])

    In [76]: np.eye(5)
    Out[76]: array([[1.,0.,0.,0.,0.],
    			   [0.,1.,0.,0.,0.],
    			   [0.,0.,1.,0.,0.],
    			   [0.,0.,0.,1.,0.],
    			   [0.,0.,0.,0.,1.]])
    			   
    In [81]: x = np.ones((2,3,4))

    In [82]: print(x)
    [[[1. 1. 1. 1.]
      [1. 1. 1. 1.]
      [1. 1. 1. 1.]]
      
      [[1. 1. 1. 1.]
       [1. 1. 1. 1.]
       [1. 1. 1. 1.]]]
       
    In [83]: x.shape
    Out[83]: (2,3,4)

    | 函数 | 说明 |
    | —————————- | ——————————————————————— |
    | np.ones_like(a) | 根据数组a的形状生成一个全1数组 |
    | np.zeros_like(a) | 根据数组a的形状生成一个全0数组 |
    | np.full_like(a,val) | 根据数组a的形状生成一个数组，每个元素值都是val |

  3. 使用NumPy中其他函数创建ndarray数组

    | 函数 | 说明 |
    | ———————— | ——————————————————— |
    | np.linspace() | 根据起止数据等间距地填充数据，形成数组 |
    | np.concatenate() | 将两个或多个数组合并成一个新的数组 |

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    In [51]: a = np.linspace(1, 10, 4) #起始位置，终止位置，希望生成几个元素

    In [52]: a
    Out[52]: array([1., 4., 7., 10.]) #1到10中间等间距分成3份

    In [53]: b = np.linspace(1, 10, 4, endpoint = False) #最后一个元素是否为生成元素中的一个

    In [54]: b
    Out[54]: array([ 1., 3.25, 5.5, 7.75]) #1到10中间等间距分成4份

    In [55]: c = np.concatenate((a,b))

    In [56]: c
    Out[56]: array([ 1., 4., 7., 10., 1., 3.25, 5.5, 7.75])

  4. 从字节流(raw bytes)中创建ndarry数组。

ndarray数组的变换

维度变换

对于创建后的ndarray数组，可以对其进行维度变换和元素类型变换。

1
a = np.ones((2,3,4) , dtype = np.int32)
方法 说明
.reshape(shape) 不改变数组元素，返回一个shape形状的数组，原数组不变
.resize(shape) 与.reshape()功能一致，但修改原数组
.swapaxes(ax1,ax2) 将数组n个维度中两个维度进行调换
.flatten() 对数组进行降维，放回折叠后的一维数组，原数组不变 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
In [105]: a.reshape((3,8))			###a.reshape
Out[105]:
array([[1,1,1,1,1,1,1,1],
	   [1,1,1,1,1,1,1,1],
	   [1,1,1,1,1,1,1,1]])
	   
In [106]: a
Out[106]:
array([[[1,1,1,1],
	    [1,1,1,1],
	    [1,1,1,1]],
	    
	   [[1,1,1,1],
	    [1,1,1,1],
	    [1,1,1,1]]])
	    
In [107]: a.resize((3,8))			###a.resize

In [108]: a
Out[108]:
array([[1,1,1,1,1,1,1,1],
	   [1,1,1,1,1,1,1,1],
	   [1,1,1,1,1,1,1,1]])

In [109]: a.flatten()				###a.flatten
Out[109]: array([1,1,1,...,1,1,1])

In [110]: a
Out[110]:
array([[1,1,1,...,1,1,1],
	   [1,1,1,...,1,1,1],
	   [1,1,1,...,1,1,1]])
	   
In [111]: b = a.flatten()

In [112]: b
Out[112]: array([1,1,1,...,1,1,1])

类型变换

1
new_a = a.astype(new_type)

astype()方法一定会创建新的数组(原始数据的一个拷贝)，即使两个类型一致。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
In [119]: a = np.ones((2,3,4),dtype = np.int)

In [120]: a
Out[120]:
array([[[1,1,1,1],
	    [1,1,1,1],
	    [1,1,1,1]],
	    
	   [[1,1,1,1],
	    [1,1,1,1],
	    [1,1,1,1]]])
	    
In [121]: b = a.astype(np.float)			###a.astype，可以改变类型

In [122]: b
Out[122]:
array([[[1.,1.,1.,1.],
	    [1.,1.,1.,1.],
	    [1.,1.,1.,1.]],
	    
	   [[1.,1.,1.,1.],
	    [1.,1.,1.,1.],
	    [1.,1.,1.,1.]]])

向列表的转换

1
Ls = a.tolist()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
In [128]: a = np.full((2,3,4),25,dtype=np.int32)

In [129]: a
Out[129]:([[[25,25,25,25],
		   [25,25,25,25],
		   [25,25,25,25]],
		  [[25,25,25,25],
		   [25,25,25,25],
		   [25,25,25,25]]])
		   
In [130]: a.tolist()			###a.tolist
Out[130]:
[[[25,25,25,25],[25,25,25,25],[25,25,25,25]],
 [[25,25,25,25],[25,25,25,25],[25,25,25,25]]]

ndarray数组的操作

数组的索引和切片

索引：获取数组中特定位置元素的过程

切片：获取数组元素子集的过程

一维数组

与python的列表类似

1
2
3
4
5
6
7
In [131]: a = np.array([9,8,7,6,5])

In [132]: a[2]
Out[132]: 7

In [133]: a[ 1 : 4 : 2]			###起始编号：终止编号(不含)：步长
Out[133]: array([8,6])

多维数组

索引

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
In [146]: a = np.arrange(24).reshape((2,3,4))

In [147]: a
Out[147]:
array([[[0,  1,  2,  3],
	    [4,  5,  6,  7],
	    [8,  9, 10, 11]],
	    
	   [[12, 13, 14, 15],
	    [16, 17, 18, 19],
	    [20, 21, 22, 23]]])

In [148]: a[1, 2, 3]
Out[148]: 23

In [149]: a[0, 1, 2]
Out[149]: 6

In [150]: a[-1,-2,-3]
Out[150]: 17

切片

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
In [146]: a = np.arrange(24).reshape((2,3,4))

In [147]: a
Out[147]:
array([[[0,  1,  2,  3],
	    [4,  5,  6,  7],
	    [8,  9, 10, 11]],
	    
	   [[12, 13, 14, 15],
	    [16, 17, 18, 19],
	    [20, 21, 22, 23]]])
	    
In [158]: a[:,1,-3]			###a[第一个维度的要求，第二个维度的要求，第三个维度的要求]
Out[158]: array([5,17])		###选取一个维度用：

In [159]: a[:,1:3,:]
Out[159]:
array([[[4,  5,  6,  7],
	    [8,  9, 10, 11]],
	    
	   [[16, 17, 18, 19],
	    [20, 21, 22, 23]]])
	    
In [160]: a[:,:,::2]		###每个维度可以使用步长跳跃切片
Out[160]:
array([[[0,2],
	    [4,6],
	    [8,10]],
	    
	   [[12,14],
	    [16,18],
	    [20,22]]])

ndarry数组的运算

数组与标量之间的运算

数组与标量之间的运算作用域数组的每一个元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
###实例：计算a与元素平均值的商

In [146]: a = np.arrange(24).reshape((2,3,4))

In [147]: a
Out[147]:
array([[[0,  1,  2,  3],
	    [4,  5,  6,  7],
	    [8,  9, 10, 11]],
	    
	   [[12, 13, 14, 15],
	    [16, 17, 18, 19],
	    [20, 21, 22, 23]]])
	    
In [169]: a.mean()
Out[169]: 11.5

In [170]: a = a / a.mean()

In [171]: a
Out[171]:
array([[[0.		   ,0.08695652,0.17391304,0.26086957],
	    [0.34782609,0.43478261,0.52173913,0.60869565],
	    [0.69565217,0.7826087 ,0.86956522,0.95652174]],
	    
	   [[1.04347826,1.13043478,1.2173913 ,1.30434783],
	    [1.39130435,1.47826087,1.56521739,1.65217391],
	    [1.73913043,1.82608696,1.91304348,2.	    ]]])

NumPy一元函数

对ndarray中的数据执行元素级运算的函数

函数 说明
np.abs(x) np.fabs(x) 计算数组各元素的绝对值
np.sqrt(x) 计算数组个元素的平方根
np.square(x) 计算数组各元素的平方
np.log(x) np.log10(x) np.log2(x) 计算数组各元素的自然对数、10底对数和2底对数
np.ceil(x) np.floor(x) 计算数组各元素的ceiling值或floor值
np.rint(x) 计算数组各元素的四舍五入值
np.modf(x) 将数组各元素的小数和整数部分以两个独立数组形式返回
np.cos(x) np.cosh(x)
np.sin(x) np.sinh(x)
np.tan(x) np.tanh(x)		 计算数组各元素的普通型和双曲型三角函数
np.exp(x) 计算数组各元素的指数值
np.sign(x) 计算数组各元素的符号值，1(+),0,-1(-)

注意数组是否被真实改变

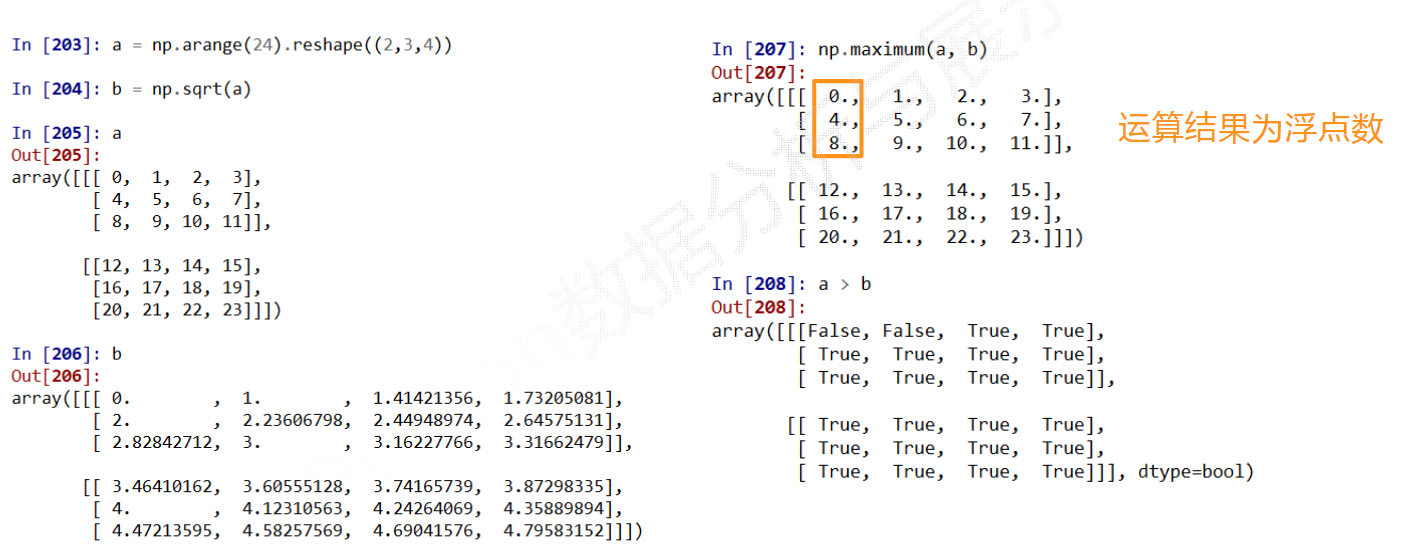
NumPy二元函数

函数 说明
+ - / * 两个数组各元素进行对应运算
np.maximum(x,y) np.fmax()
np.minimum(x,y) np.fmin()		 元素级的最大值、最小值计算
np.mod(x,y) 元素级的模运算
np.copysign(x,y) 将数组y中各元素的符号赋值给数组x对应元素
> < >= <= == != 算数比较，产生布尔型数组

小结

数据存储

一维：CSV文件存取

CSV是一种常见的文件格式，用来存储批量数据

局限性：只能有效存储一维和二维数组

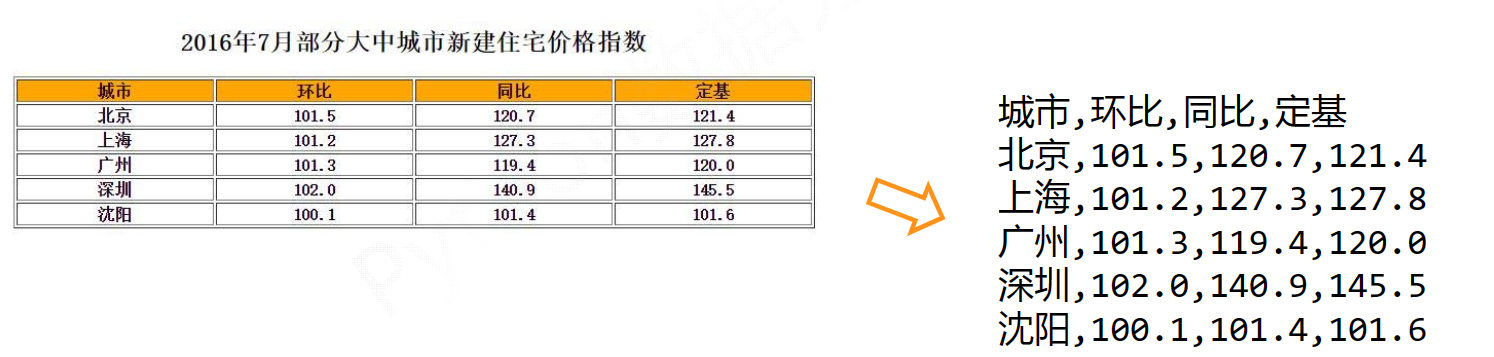
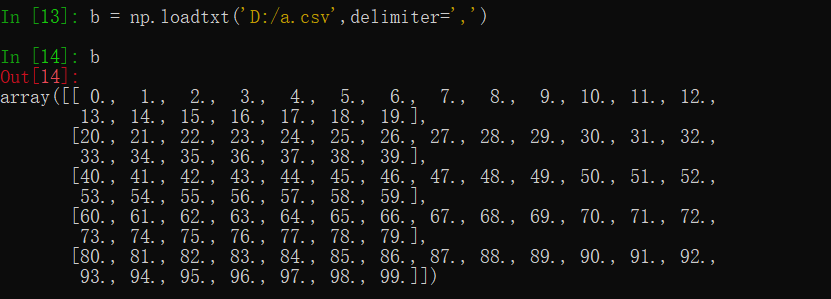
savetxt

1
2
3
4
5
np.savetxt(frame,array,fmt='%.18e',delimiter=None)
#frame: 文件、字符串或产生器，可以是.gz或.bz2的压缩文件
#array：存入文件的数组
#fmt: 写入文件的格式，例如：%d %.2f %.18e
#delimiter: 分割字符串，默认是任何空格
1
a = np.arange(100).reshape(5,20)

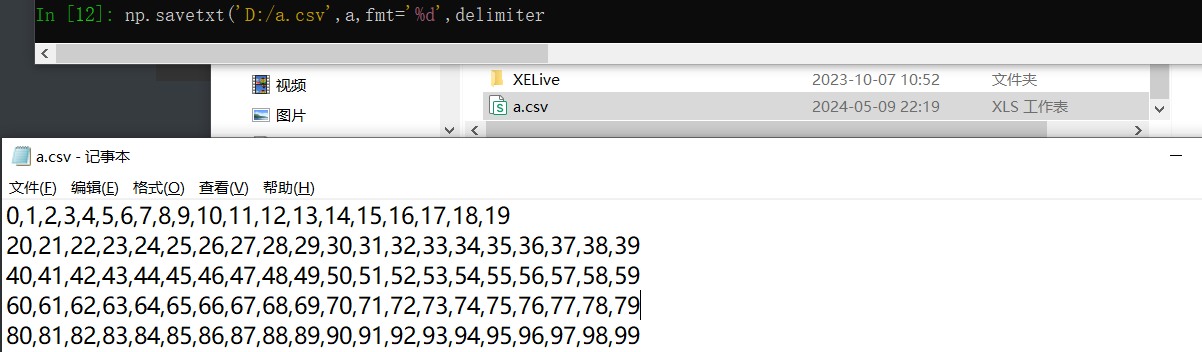
loadtxt

1
2
3
4
5
np.loadtxt(frame,dtype=np.float,delimiter=None,unpack=False)
#frame: 文件、字符串或产生器，可以是.gz或.bz2的压缩文件
#dtype：数据类型，可选
#delimiter：分割字符串，默认是任何空格
#unpack：如果True，读入属性将分别写入不同变量

多维数据存取

tofile

1
2
3
4
5
a.tofile(frame,sep='',format='%s')

# frame : 文件、字符串
# sep   ：数据分割字符串，如果是空串，写入文件为二进制
# format：写入数据的格式
1
2
In [125]: a = np.arange(100).reshape(5,10,2)
In [126]: a.tofile("b.dat",sep=",",format="%d")
1
2
3
4
In [127]: a = np.arange(100).reshape(5,10,2)
In [128]: a.tofile("b.dat",format="%d")
#如果不知道分割符，则生成二进制文件，二进制文件占用更小的空间
#看不到内容，只能作为数据备份的一种方式

fromfile

1
2
3
4
5
np.fromfile(frame,dtype=float,cont=-1,sep='')
# frame:文件、字符串
# dtype:读取的数据类型
# count:读入元素个数，-1表示读入整个文件
# sep:数据分割字符串，如果是空串，写入文件为二进制

文本文件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
In [129]: a = np.arange(100).reshape(5,10,2)
In [130]: a.tofile("b.dat",sep=",",format='%d')
In [131]: c = np.fromfile("b.dat",dtype=np.int,sep=",")
In [132]: c
Out[132]: array([0,1,2,...,97,98,99])
In [133]: c = np.fromfile("b.dat",dtype=np.int,sep=",").reshape(5,10,2)
In [134]: c
Out[134]:
array([[[0,1],
	    [2,3],
	    [4,5],
	    ...,
	    [14,15],
	    [16,17],
	    [18,19]],

二进制文件

1
2
3
4
5
6
7
8
9
10
11
12
In [125]: a = np.arange(100).reshape(5,10,2)
In [136]: a.tofile("b.dat",format='%d')
In [137]: c = np.fromfile("b.dat",dtype=np.int).reshape(5,10,2)
In [138]: c
Out[138]:
array([[[0,1],
	    [2,3],
	    [4,5],
	    ...,
	    [14,15],
	    [16,17],
	    [18,19]],

注意

  • 该方法需要读取时知道存入文件时数组的维度和元素类型
  • a.tofile()和np.fromfile()需要配合使用
  • 可以通过元素据文件来存储额外信息

NumPy的便捷文件存取

1
2
3
4
5
np.save(fname,array)或np.savez(fname,array)
# frame:文件名，以.npy为扩展名，压缩扩展名为.npz
# array:数组变量
np.load(fname)
# fname:文件名，以.npy为扩展名，压缩扩展名为.npz

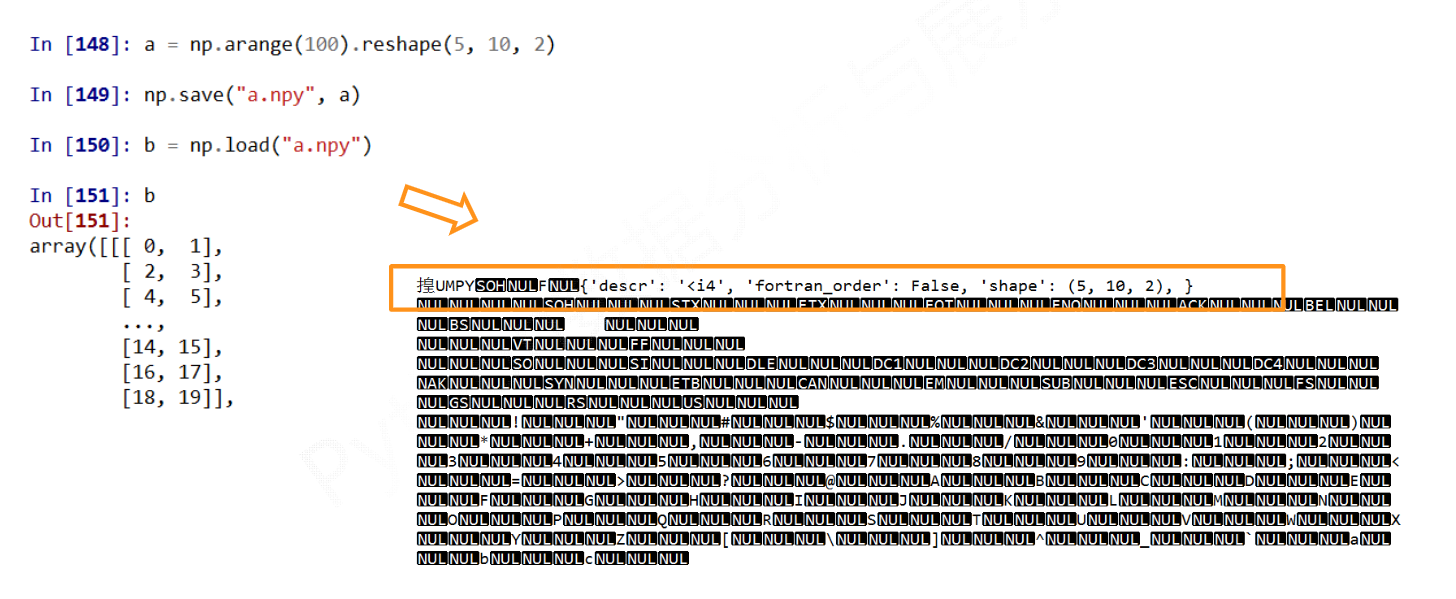
NumPy函数

随机数函数子库

函数 说明
rand(d0,d1,..,dn) 根据d0-dn创建随机数数组，浮点数，[0,1)，均匀分布
randn(d0,d1,..,dn) 根据d0-d n创建随机数数组，标准正态分布
randint(low[,high,shape]) 根据shape创建随机整数或整数数组，范围时[low,high)
seed(s) 随机数种子，s时给定的种子值
函数 说明
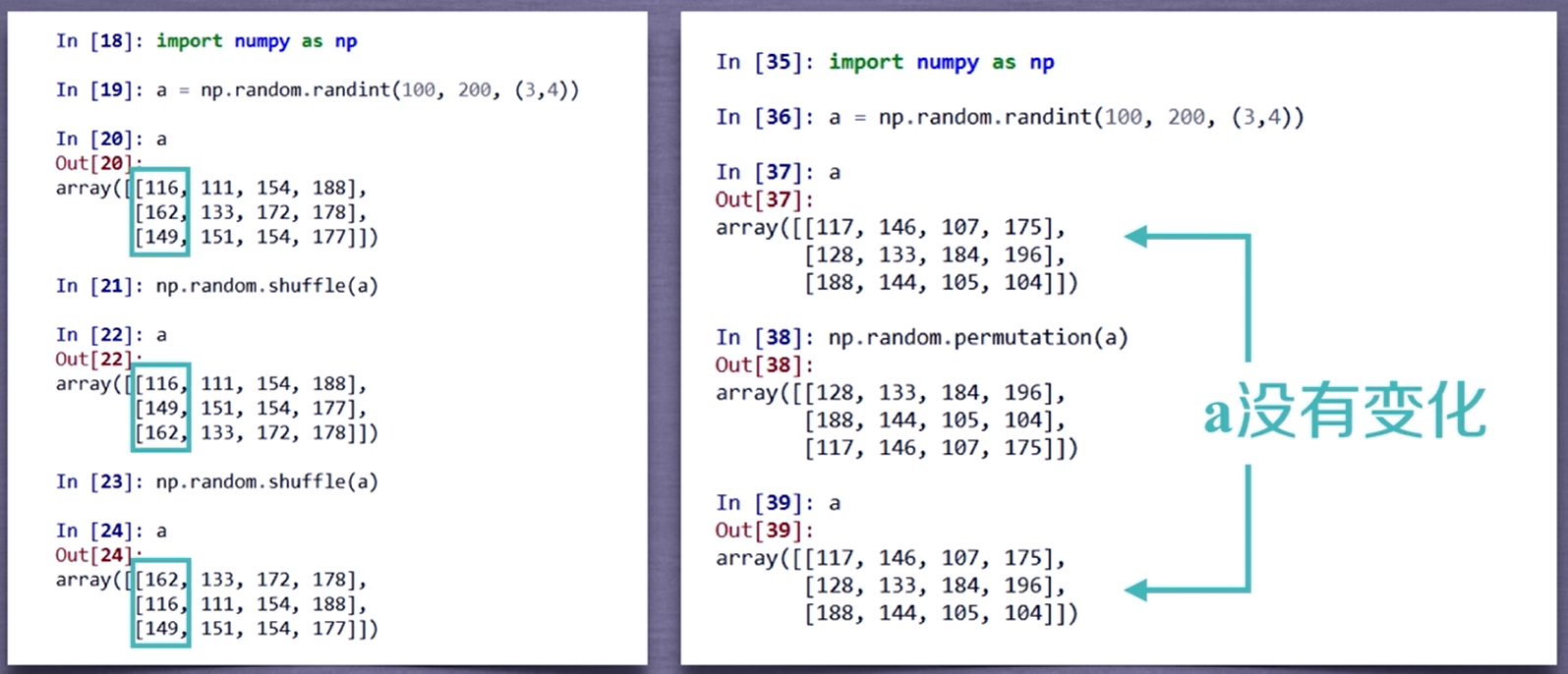
shuffle(a) 根据数组a的第1轴进行随排列，改变数组x
permutation(a) 根据数组a的第一轴产生一个新的乱序数组，不改变数组x
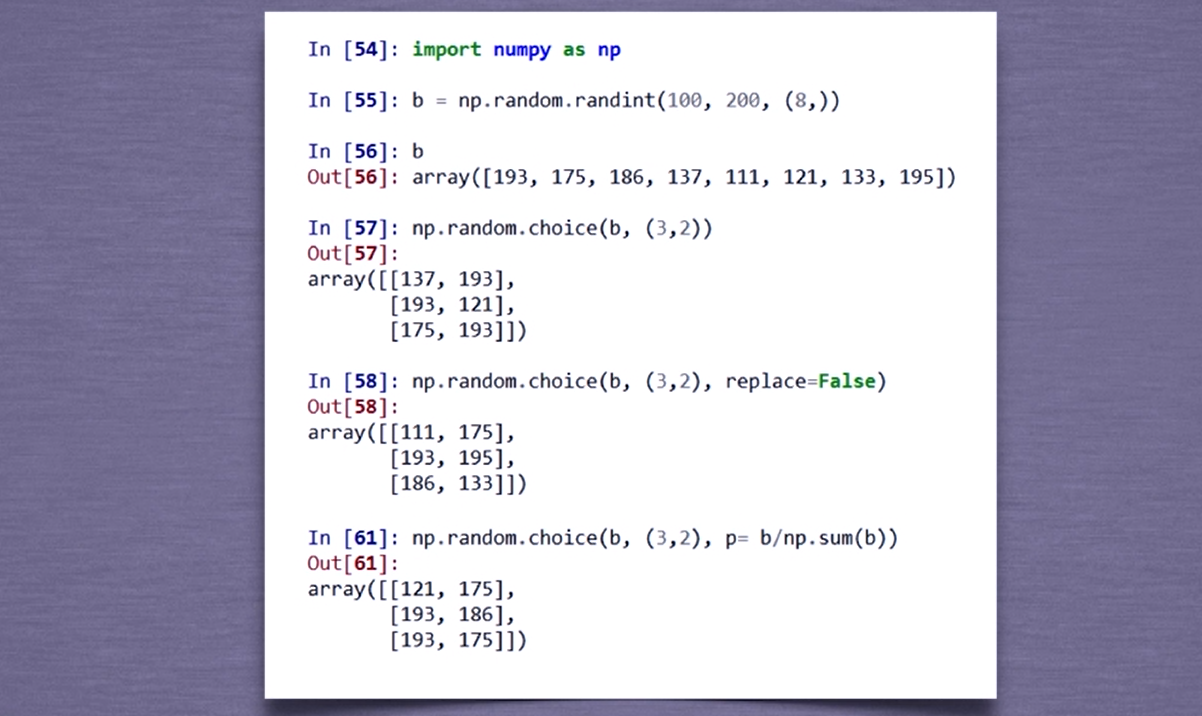
choice(a[,size,replace,p]) 从一维数组中以概率p抽取元素，形成size形状新数组
replace表示是否可以重用元素，默认为False
函数 说明
uniform(low,high,size) 产生具有均匀分布的数组，low起始值，high结束值，size形状
normal(loc,scale,size) 产生具有正态分布的数组，loc均值，scale标准差，size形状
poisson(lam,size) 产生具有泊松分布的数组，lam随机事件发生率，size形状

统计函数

NumPy直接提供的统计累函数，可以直接np.*使用

函数 说明
sum(a,axis=None) 根据给定轴axis计算数组a相关元素之和，axis整数或元组
mean(a,axis=None) 根据给定轴axis计算数组相关元素的期望，axis整数或元组
average(a,axis=None,weights=None) 根据给定轴axis计算数组a相关元素的加权平均值
std(a,axis=None) 根据给定轴axis计算数组a相关元素的标准差
var(a,axis=None) 根据给定轴axis计算数组a相关元素的方差
函数 说明
min(a) max(a) 计算数组a中元素的最小值、最大值
argmin(a) argmax(a) 计算数组a中元素最小值、最大值的降一维后下标
unravel_index(index,shape) 根据shape将一维下标index转换成多维下标
ptp(a) 计算数组a中元素最大值与最小值的差
median(a) 计算数组a中元素的中位数(中值)

梯度函数

函数 说明
np.gradient(f) 计算数组f中元素的梯度，当f为多维时，返回每个维度梯度

梯度：连续值之间的变化率，即斜率

XY坐标轴连续三个X坐标对应的Y轴值：a,b,c，其中，b的梯度是：(c-a)/2

如果数组是n维，的那么gradient生成n个数组

图像的手绘效果

图像的数组表示

图像一般使用RGB色彩模式，即每个像素点的颜色由红(R)、绿(G)、蓝(B)组成，其中每个通道的取值范围均为0-255，叠加起来色彩空间为255^3。RGB形成的颜色包括了人类视力所能感知的所有颜色。

PIL库

一个具有强大图像处理能力的第三方库。

1
2
pip install pillow	#安装
from PIL import Image #Image是PIL库代表一个图像的类（对象）
1
2
3
4
5
6
In [64]:from PIL import Image
In [65]:import numpy as np
In [66]:im = np.array(Image.open("D:/pycodes/demo.jpg"))
In [67]:print(im.shape,im.dtype)
(669,1012,3)uint8
###图像是一个三维数组，维度分别是高度、宽度和像素RGB值

图像的变换

读入图像后，获得像素RGB值，修改后保存为新的文件。

1
2
3
4
5
6
7
8
In [81]:from PIL import Image
In [82]:import numpy as np
In [83]:a = np.array(Image.open("D:/demo.jpg"))
In [84]:print(a.shape,a.dtype)
(669,1012,3)uint8
In [85]:b = [255,255,255]-a
In [86]:im = Image.fromarray(b.astype('uint8'))
In [87]:im.save("D:/demo1.jpg")

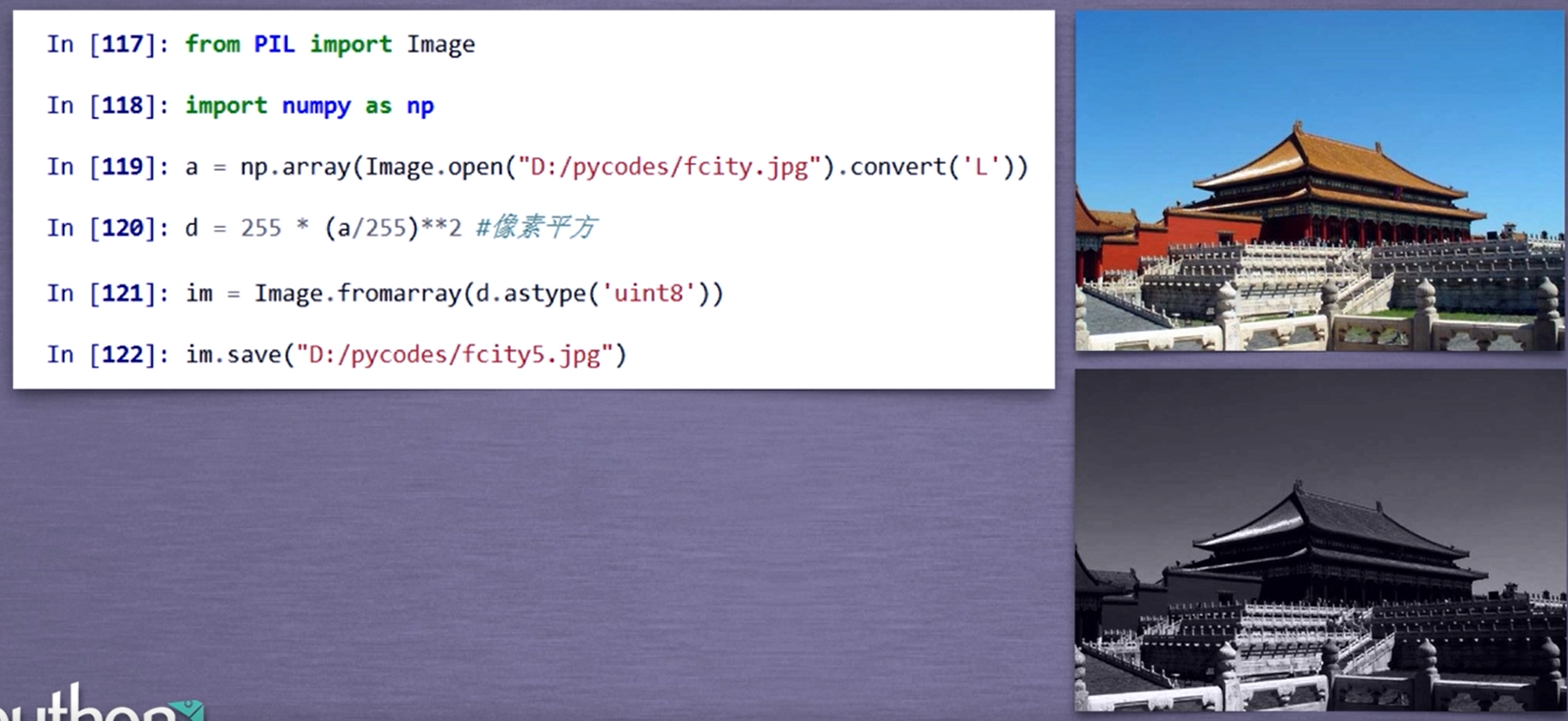
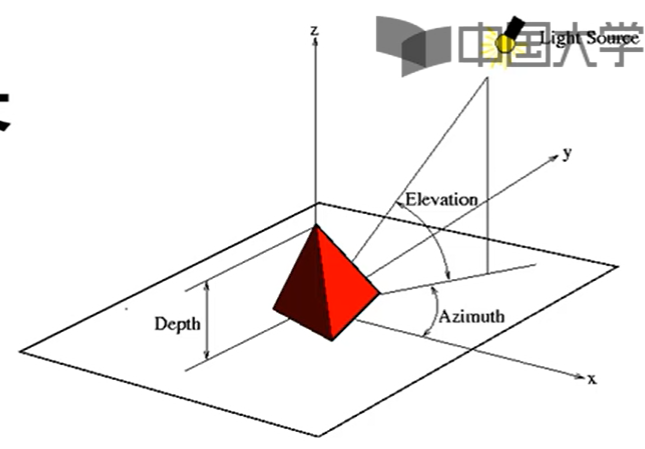
“图像手绘效果”实例分析

手绘效果几个特征：黑白灰色，线条比较重，相同或相近色彩趋于白色，略有光源效果

利用像素之间的梯度值和虚拟深度值对图像进行重构

根据灰度变化来模拟人类视觉明暗程度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
from PIL import Image
import numpy as np

a = np.asarray(Image.open('G:/1.jpg').convert('L')).astype('float')

depth = 10.								#预设深度值为10，取值范围(0-100)
grad = np.gradient(a)					 #取图像灰度的梯度值，表示灰度的变化率
grad_x,grad_y = grad					 #分别取横纵图像梯度值
grad_x = grad_x*depth/100.
grad_y = grad_y*depth/100.				 #根据深度调整x和y方向的梯度值

A = np.sqrt(grad_x**2 + grad_y**2 + 1.)	  #构造x和y轴梯度的三维归一单位坐标系

uni_x = grad_x/A
uni_y = grad_y/A
uni_z = 1./A

vec_el = np.pi/2.2						 #光源的俯视角度，弧度值
vec_az = np.pi/4.						 #光源的方位角度，弧度值
dx = np.cos(vec_el)*np.cos(vec_az)		   #光源对x轴的影响，np.cos(vec_el)为单位光线在地平面的投影长度
dy = np.cos(vec_el)*np.sin(vec_az)		   #光源对y轴的影响
dz = np.sin(vec_el)						  #光源对z轴的影响

b = 255*(dx*uni_x +dy*uni_y +dz*uni_z)	   #光源归一化，梯度与光源相互作用，将梯度转化为灰度？？？？
b = b.clip(0,255)						 #为避免数据越界，将生成的灰度值裁剪至0-255区间

im = Image.fromarray(b.astype('uint8'))		#重构图像
im.save('G:\\1hd.jpg')
人工智能 > 数据分析与展示
#数据分析 #分析工具
NumPy库入门
http://example.com/2024/04/30/20240430_numPy/
作者
XuanYa
发布于
2024年4月30日
许可协议