序列模型

自回归模型

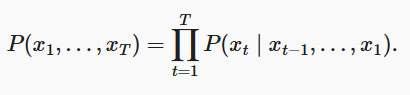
1. 时间步 1：初始概率
   • P(x1)：表示序列的第一个元素 x1 的概率，没有依赖其他事件（条件为空）。
   • 这是序列生成的起点。
2. 时间步 2：条件概率
   • P(x2∣x1)：在 x1已经发生的条件下，x2发生的概率。
   • 这里体现了序列数据的依赖性，x2的出现依赖于 x1。
3. 时间步 3：条件概率
   • P(x3∣x2,x1)：在 x1和 x2已经发生的条件下，x3发生的概率。
4. *一般情况：时间步 tt
   • P(xt∣xt−1,…,x1)：表示第 t 个时间步的值 xt 发生的概率，条件是之前的所有时间步值 xt−1,…,x1 都已经发生。
5. 递归性质：乘积展开
   • 联合概率 P(x1,x2,…,xT) 是从起点到终点，每一步条件概率的累积，公式通过乘法累积这种依赖关系。

马尔可夫模型

求

$$P(x_t∣x_{t−1})P(x_{t+1} \mid x_{t-1}) = \sum_{x_t} P(x_{t+1} \mid x_t) P(x_t \mid x_{t-1})$$

---

分解的核心思想

1. 条件概率的链式法则： $$P(x_{t+1}, x_t \mid x_{t-1}) = P(x_{t+1} \mid x_t, x_{t-1}) P(x_t \mid x_{t-1})$$

• $$P(x_{t+1} \mid x_{t-1}) = \sum_{x_t} P(x_{t+1}, x_t \mid x_{t-1})$$

1. 马尔可夫性假设： $$P(x_{t+1} \mid x_t, x_{t-1}) = P(x_{t+1} \mid x_t)$$

1. 条件独立性简化： $$P(x_{t+1} \mid x_{t-1}) = \sum_{x_t} P(x_{t+1} \mid x_t) P(x_t \mid x_{t-1})$$

---

分解步骤解释

原始公式：

$$P(x_{t+1} \mid x_{t-1}) = \frac{\sum_{x_t} P(x_{t+1}, x_t, x_{t-1})}{P(x_{t-1})}$$

1. 分解联合概率： $$P(x_{t+1}, x_t, x_{t-1}) = P(x_{t+1} \mid x_t, x_{t-1}) P(x_t \mid x_{t-1}) P(x_{t-1})$$ 代入公式并消去分母 $$P(x_{t-1})$$ ，得： $$P(x_{t+1} \mid x_{t-1}) = \sum_{x_t} P(x_{t+1} \mid x_t, x_{t-1}) P(x_t \mid x_{t-1})$$

1. 马尔可夫性假设：

   假设

   $$P(x_{t+1} \mid x_t, x_{t-1}) = P(x_{t+1} \mid x_t)$$

   公式简化为：

   $$P(x_{t+1} \mid x_{t-1}) = \sum_{x_t} P(x_{t+1} \mid x_t) P(x_t \mid x_{t-1})$$

问题

是的，从你的描述来看，这可以理解为超过滞后窗口大小 n 的 n-步预测通常效果会显著下降

---

1. 为什么超过 n 的 n-步预测效果会显著下降？

假设滞后窗口长度 n 表示模型输入特征的时间步数量（如 [xt−n+1,xt−n+2,…,xt][x_{t-n+1}, x_{t-n+2}, \dots, x_t]），那么：

1. 窗口长度的限制：
   • 模型只能基于滞后窗口提供的 n 个历史点进行预测。
   • 如果时间序列存在远期依赖（例如 x_t 与 x_{t-k} 相关，k > n），模型无法感知这些长时间依赖，导致预测不准确。
2. 递归预测的误差累积：
   • n-步预测需要递归使用模型的输出作为下一步的输入。
   • 每次递归预测都会引入小误差，误差在多次递归后迅速放大，使得长时间步预测的效果几乎失去参考价值。
3. 时间序列的特性：
   • 如果时间序列具有强随机性或复杂的长期依赖（例如金融市场、天气变化），模型难以捕获这些模式，超过 n的预测值会趋于偏离真实分布。

---

2. 滞后窗口 n 和预测步长 k 的关系

从滞后窗口 n 的角度分析，预测步长 k 的效果可分为以下几种情况：

(1) k≤n：短步预测

• 效果：预测效果通常较好，因为模型能够利用窗口内的所有信息，捕获当前点 x_t 和未来点 xt+kx_{t+k} 的相关性。
• 原因：模型的输入窗口长度 n 足够涵盖预测目标的依赖关系。

(2) k > n：长步预测

• 效果：预测效果显著下降，可能完全偏离真实趋势。

• 原因

  ：

  • 窗口信息不足：模型输入只包含最近 n 个点的信息，缺乏对更远依赖关系的感知。
  • 误差累积：长步预测需要递归使用预测值作为输入，每一步都会放大误差。

---

3. 为什么会有这种现象？（理论原因）

(1) 马尔可夫性假设的局限性

• 在滞后窗口 n 的基础上，模型通常假设序列满足“有限阶马尔可夫性”，即未来 x_{t+k} 的分布仅与最近的 n个点相关： $$P(x_{t+k} \mid x_t, x_{t-1}, \dots, x_{t-n+1})$$

• 如果时间序列的真实依赖关系超出了窗口 nn，模型将无法准确捕获这些远期关系。

(2) 递归误差放大

递归预测中，每一步预测都依赖于之前的预测值作为输入：

$$\hat{x}_{t+k} = f(\hat{x}_{t+k-1}, \hat{x}_{t+k-2}, \dots, \hat{x}_{t+k-n})$$

• 当 k>nk > n 时，所有输入可能完全是预测值。
• 如果预测值中存在小误差，每次递归会将误差累积并放大。

---

4. 长步预测是否完全无用？

虽然k > n 的预测效果通常较差，但是否“无用”取决于以下几个因素：

(1) 时间序列的特性

• 如果时间序列中存在明显的长期趋势或周期性，长步预测可能仍有意义。例如：
  • 气候数据：长期温度的趋势通常稳定，可以通过模型捕获。
  • 经济数据：季度 GDP 或消费指数可能呈现周期性。

(2) 模型的复杂性

• 简单的滞后窗口可能无法捕获远期依赖，但复杂的模型（如 RNN、LSTM、Transformer）可以更好地学习长时间依赖，提高 k > n 的预测效果。

(3) 预测的目的

• 如果长步预测仅用于捕获整体趋势或方向，而不是精确值，那么即使误差较大，也可能在某些场景中具有参考价值。

---

5. 如何改进长步预测？

1. 引入更复杂的模型

   • 使用能捕获长时间依赖的序列模型，如 RNN、LSTM、GRU 或 Transformer。
   • 这些模型通过循环或注意力机制记住更多历史信息，超越简单的滞后窗口。

2. 减少递归误差

   • 直接预测：让模型直接输出未来 kk-步的值，而不是逐步递归生成：

     $$[\hat{x}_{t+1}, \hat{x}_{t+2}, \dots, \hat{x}_{t+k}] = f(x_{t-n+1}, \dots, x_t)$$

   • 混合策略：结合真实值和预测值作为输入（如 Teacher Forcing）。

3. 调整损失函数

   • 设计针对长步预测的损失函数，鼓励模型更准确地拟合远期目标。

---

6. 总结

• 超过滞后窗口 n 的预测步长 k > n，通常由于信息不足和误差累积而变得不可靠。
• 在简单模型中，这种现象尤其明显，因此需要合理选择窗口大小 n 和预测步长 k。
• 长步预测是否“无用”取决于时间序列的特性、模型能力以及预测任务的具体需求。复杂模型（如 LSTM、Transformer）可以部分缓解这种问题。