语言模型和数据集

马尔可夫模型和n元语法

1. 背景：马尔可夫性假设

  • 马尔可夫性假设是语言建模中的核心思想之一。

  • 假设序列中当前状态只依赖于有限个历史状态，可以减少计算复杂性。

  • 公式中提到的分布：

    根据马尔可夫性假设简化为：

    , 即，序列的下一个状态只依赖于当前状态，而与更久远的历史无关。

2. 公式解析与语法模型

(1) 通用的链式法则

  • 根据链式法则，任意序列 可以展开为：
  • 这是最完整的公式，假设每个词都可能依赖于前面所有的词。

(2) 简化公式：马尔可夫假设

根据不同阶的马尔可夫性假设，可以逐步简化：

  1. 一元语法（unigram）模型：

    • 意义：忽略词与词之间的关系，适合简单统计和快速计算。

    • 缺点：不能捕捉词与词之间的语法或上下文关系。

  2. 二元语法（bigram）模型：

    • 意义：只考虑词对之间的关系，比如捕捉到「deep learning」这种词对的依赖性。

    • 优点：比一元模型更能反映词之间的语法关系。

    • 缺点：无法捕捉更长的上下文依赖。

  3. 三元语法（trigram）模型：

    • 意义：能够捕捉三元词组之间的依赖性，比如「state of the」。

    • 优点：能捕捉更长的依赖。

    • 缺点：当序列长度较大时，计算复杂度仍然较高，且数据稀疏性更严重。

3. 示例

假设序列为：「I love deep learning」，概率计算如下：

一元语法模型：

二元语法模型：

三元语法模型：

4. 总结

  • 一元语法假设独立性，计算简单，但无法捕捉任何上下文信息。
  • 二元语法假设当前词只依赖前一个词，适合捕捉词对关系，计算效率较高。
  • 三元语法扩展了依赖范围，但面临计算复杂度和数据稀疏的问题。

自然语言统计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import random
import torch
from d2l import torch as d2l

tokens = d2l.tokenize(d2l.read_time_machine())
# 因为每个文本行不一定是一个句子或一个段落，因此我们把所有文本行拼接到一起
corpus = [token for line in tokens for token in line]
vocab = d2l.Vocab(corpus)
vocab.token_freqs[:10]

######
[('the', 2261),
 ('i', 1267),
 ('and', 1245),
 ('of', 1155),
 ('a', 816),
 ('to', 695),
 ('was', 552),
 ('in', 541),
 ('that', 443),
 ('my', 440)]

正如我们所看到的，最流行的词看起来很无聊， 这些词通常被称为停用词（stop words），因此可以被过滤掉。 尽管如此，它们本身仍然是有意义的，我们仍然会在模型中使用它们。 此外，还有个明显的问题是词频衰减的速度相当地快。 例如，最常用单词的词频对比，第10个还不到第1个的1/5。 为了更好地理解，我们可以画出的词频图：

1
2
3
freqs = [freq for token, freq in vocab.token_freqs]
d2l.plot(freqs, xlabel='token: x', ylabel='frequency: n(x)',
         xscale='log', yscale='log')

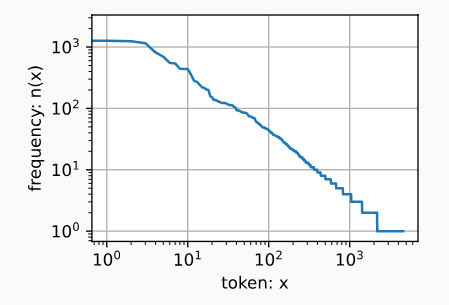
image-20241128153852275

齐普夫定律 (Zipf’s Law)

齐普夫定律是一种描述自然语言中的词频分布规律的经验法则，它由语言学家乔治·齐普夫 (George Zipf) 提出。这一定律表明，在一段文本或语料中，单词的出现频率与其频率排名成反比。

公式

其中：

  • f(r)：单词的出现频率（词频）。
  • r：单词的频率排名。
  • s：幂指数（通常在自然语言中约为 1）。
  • ∝：表示“成正比”。

可以简单表达为：

直观解释

  • 自然语言文本中的单词分布非常不均匀。
  • 高频词（如“the”、“of”、“and”）出现的次数远远多于低频词。
  • 齐普夫定律的核心观点
    • 排名为第 1 的单词（最高频单词）的出现次数，约等于排名第 2 的单词的 2 倍，约等于排名第 3 的单词的 3 倍，依此类推。
    • 例如：
      • 最高频单词出现 1000 次；
      • 排名第 2 的单词出现约 500 次；
      • 排名第 3 的单词出现约 333 次。

自然语言中的应用

(1) 高频词与低频词
  • 自然语言中，大量的单词只出现过一次或几次（称为“长尾单词”）。
  • 高频词如“the”、“is”、“of”占据了语料库的大部分词频，但信息量较少。
  • 低频词信息丰富，但在整个语料库中数量很少。
(2) 词汇覆盖问题
  • 齐普夫定律表明，用少量的高频词可以覆盖大部分的语料。
  • 示例：
    • 前 1000 个高频单词可能覆盖文本中 80% 的单词出现次数。
(3) 数据稀疏问题
  • 长尾单词的存在使得构建语言模型时会面临数据稀疏问题，许多低频词甚至在训练集中没有出现。

局限性

  • 不能解释所有语言中的词频分布规律
  • 对长尾单词的预测能力有限
  • 无法直接量化单词的语义贡献

等价于

其中α是刻画分布的指数，c是常数。 这告诉我们想要通过计数统计和平滑来建模单词是不可行的， 因为这样建模的结果会大大高估尾部单词的频率，也就是所谓的不常用单词。 那么其他的词元组合，比如二元语法、三元语法等等，又会如何呢？ 我们来看看二元语法的频率是否与一元语法的频率表现出相同的行为方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
bigram_tokens = [pair for pair in zip(corpus[:-1], corpus[1:])]
bigram_vocab = d2l.Vocab(bigram_tokens)
bigram_vocab.token_freqs[:10]

######
[(('of', 'the'), 309),
 (('in', 'the'), 169),
 (('i', 'had'), 130),
 (('i', 'was'), 112),
 (('and', 'the'), 109),
 (('the', 'time'), 102),
 (('it', 'was'), 99),
 (('to', 'the'), 85),
 (('as', 'i'), 78),
 (('of', 'a'), 73)]

这里值得注意：在十个最频繁的词对中，有九个是由两个停用词组成的， 只有一个与“the time”有关。 我们再进一步看看三元语法的频率是否表现出相同的行为方式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
trigram_tokens = [triple for triple in zip(
    corpus[:-2], corpus[1:-1], corpus[2:])]
trigram_vocab = d2l.Vocab(trigram_tokens)
trigram_vocab.token_freqs[:10]

######
[(('the', 'time', 'traveller'), 59),
 (('the', 'time', 'machine'), 30),
 (('the', 'medical', 'man'), 24),
 (('it', 'seemed', 'to'), 16),
 (('it', 'was', 'a'), 15),
 (('here', 'and', 'there'), 15),
 (('seemed', 'to', 'me'), 14),
 (('i', 'did', 'not'), 14),
 (('i', 'saw', 'the'), 13),
 (('i', 'began', 'to'), 13)]

最后，我们直观地对比三种模型中的词元频率：一元语法、二元语法和三元语法。

1
2
3
4
5
bigram_freqs = [freq for token, freq in bigram_vocab.token_freqs]
trigram_freqs = [freq for token, freq in trigram_vocab.token_freqs]
d2l.plot([freqs, bigram_freqs, trigram_freqs], xlabel='token: x',
         ylabel='frequency: n(x)', xscale='log', yscale='log',
         legend=['unigram', 'bigram', 'trigram'])

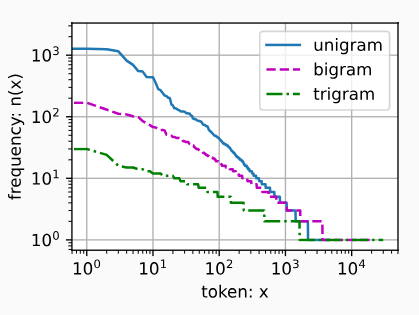
image-20241128162424131

总结

  1. 除了一元语法词，单词序列似乎也遵循齐普夫定律
  2. 词表中n元组的数量并没有那么大，这说明语言中存在相当多的结构， 这些结构给了我们应用模型的希望
  3. 很多n元组很少出现，这使得拉普拉斯平滑非常不适合语言建模。 作为代替，我们将使用基于深度学习的模型

读取长序列数据

image-20241128163004487

随机采样

在随机采样中，每个样本都是在原始的长序列上任意捕获的子序列。 在迭代过程中，来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻。 对于语言建模，目标是基于到目前为止我们看到的词元来预测下一个词元， 因此标签是移位了一个词元的原始序列。

缺点：

  • 缺乏上下文连续性
  • 数据冗余问题
  • 训练样本分布不均匀
  • 时间序列的顺序性丢失
  • 不适合生成式任务
  • 模型收敛较慢
  • 随机性可能导致结果不稳定
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#从数据中随机生成一个小批量。 在这里，参数batch_size指定了每个小批量中子序列样本的数目， 参数num_steps是每个子序列中预定义的时间步数。

def seq_data_iter_random(corpus, batch_size, num_steps):  #@save
    """使用随机抽样生成一个小批量子序列"""
    # 从随机偏移量开始对序列进行分区，随机范围包括num_steps-1
    corpus = corpus[random.randint(0, num_steps - 1):]
    # 减去1，是因为我们需要考虑标签
    num_subseqs = (len(corpus) - 1) // num_steps
    # 长度为num_steps的子序列的起始索引
    initial_indices = list(range(0, num_subseqs * num_steps, num_steps))
    # 在随机抽样的迭代过程中，
    # 来自两个相邻的、随机的、小批量中的子序列不一定在原始序列上相邻
    random.shuffle(initial_indices)

    def data(pos):
        # 返回从pos位置开始的长度为num_steps的序列
        return corpus[pos: pos + num_steps]

    num_batches = num_subseqs // batch_size
    for i in range(0, batch_size * num_batches, batch_size):
        # 在这里，initial_indices包含子序列的随机起始索引
        initial_indices_per_batch = initial_indices[i: i + batch_size]
        X = [data(j) for j in initial_indices_per_batch]
        Y = [data(j + 1) for j in initial_indices_per_batch]
        yield torch.tensor(X), torch.tensor(Y)
        
        
my_seq = list(range(35))
for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
    print('X: ', X, '\nY:', Y)
    
######
X:  tensor([[13, 14, 15, 16, 17],
        [28, 29, 30, 31, 32]])
Y: tensor([[14, 15, 16, 17, 18],
        [29, 30, 31, 32, 33]])
X:  tensor([[ 3,  4,  5,  6,  7],
        [18, 19, 20, 21, 22]])
Y: tensor([[ 4,  5,  6,  7,  8],
        [19, 20, 21, 22, 23]])
X:  tensor([[ 8,  9, 10, 11, 12],
        [23, 24, 25, 26, 27]])
Y: tensor([[ 9, 10, 11, 12, 13],
        [24, 25, 26, 27, 28]])
封装类

随机采样：用于需要数据多样性、上下文依赖性较低的任务。

顺序采样：用于需要捕获序列上下文的任务，例如语言建模或时间序列预测。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#提供一个统一接口，用于加载和生成序列数据。
#支持随机采样和顺序采样两种数据生成方式。
#自动处理语料的加载、预处理和子序列划分
#可以通过扩展 data_iter_fn 来支持更多类型的采样策略，例如带权重的随机采样或滑动窗口采样。

class SeqDataLoader:  #@save
    """加载序列数据的迭代器"""
    def __init__(self, batch_size, num_steps, use_random_iter, max_tokens):
        if use_random_iter:
            self.data_iter_fn = d2l.seq_data_iter_random
        else:
            self.data_iter_fn = d2l.seq_data_iter_sequential
        self.corpus, self.vocab = d2l.load_corpus_time_machine(max_tokens)
        self.batch_size, self.num_steps = batch_size, num_steps

    def __iter__(self):
        return self.data_iter_fn(self.corpus, self.batch_size, self.num_steps)
封装类
1
2
3
4
5
6
7
8
9
10
11
#返回值：数据迭代器：生成训练用的小批量数据。词汇表：用于词元和索引的映射。
#提供统一接口，加载语料并生成数据迭代器。
#支持随机采样和顺序采样两种方式。
#随机采样适合多样性较高的任务，顺序采样适合上下文依赖性较强的任务。

def load_data_time_machine(batch_size, num_steps,  #@save
                           use_random_iter=False, max_tokens=10000):
    """返回时光机器数据集的迭代器和词表"""
    data_iter = SeqDataLoader(
        batch_size, num_steps, use_random_iter, max_tokens)
    return data_iter, data_iter.vocab
人工智能 > 深度学习
#深度学习 #数据处理
语言模型和数据集
http://example.com/2024/11/28/20241128_语言模型和数据集/
作者
XuanYa
发布于
2024年11月28日
许可协议